Introducción
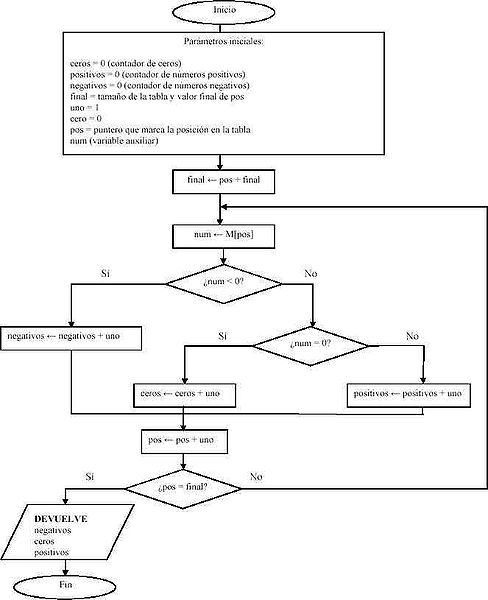
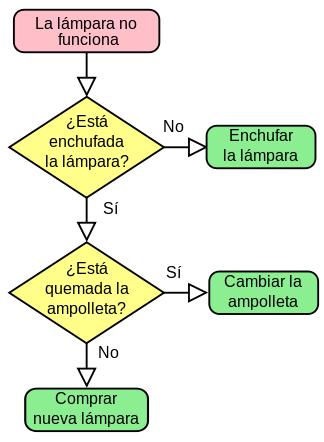
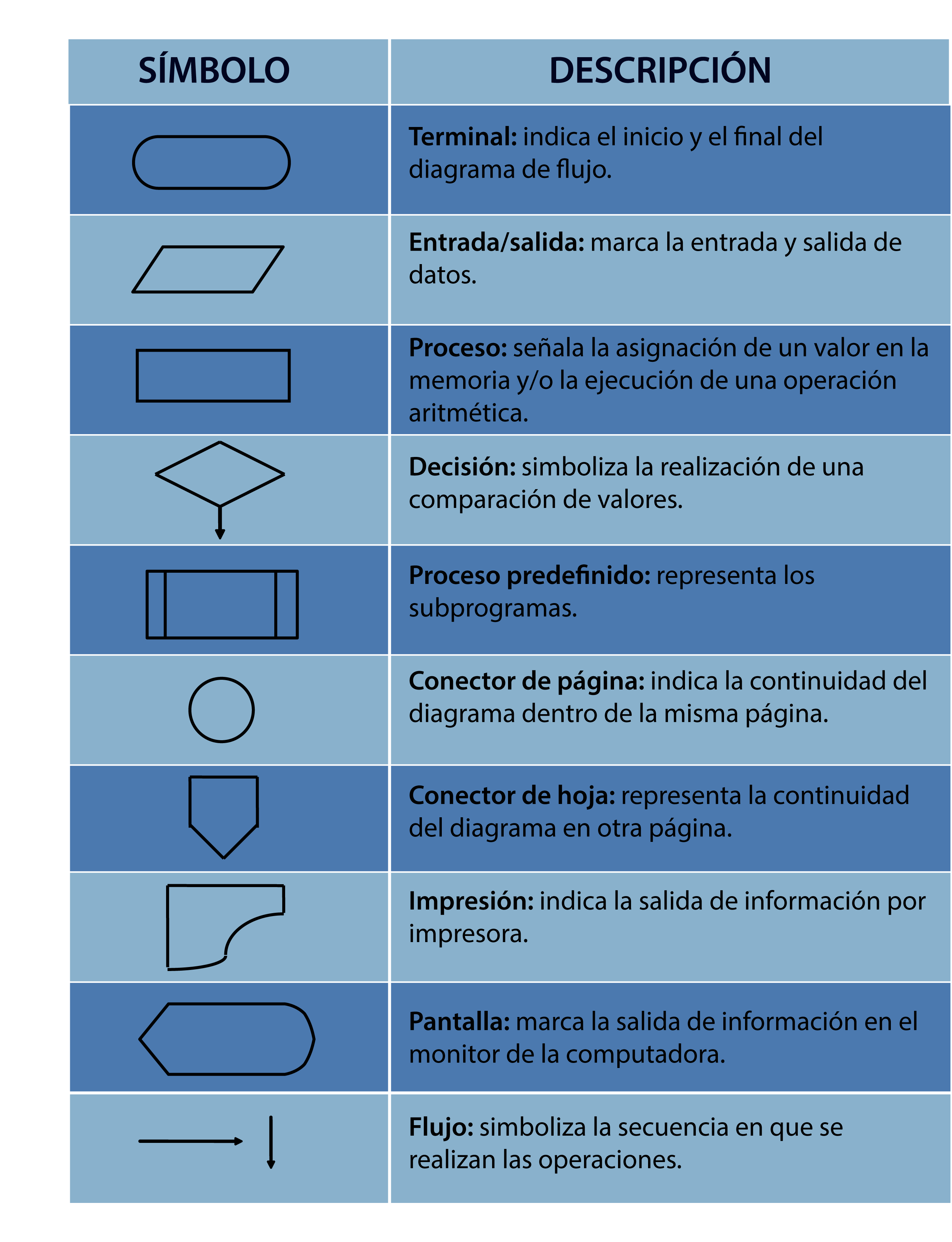
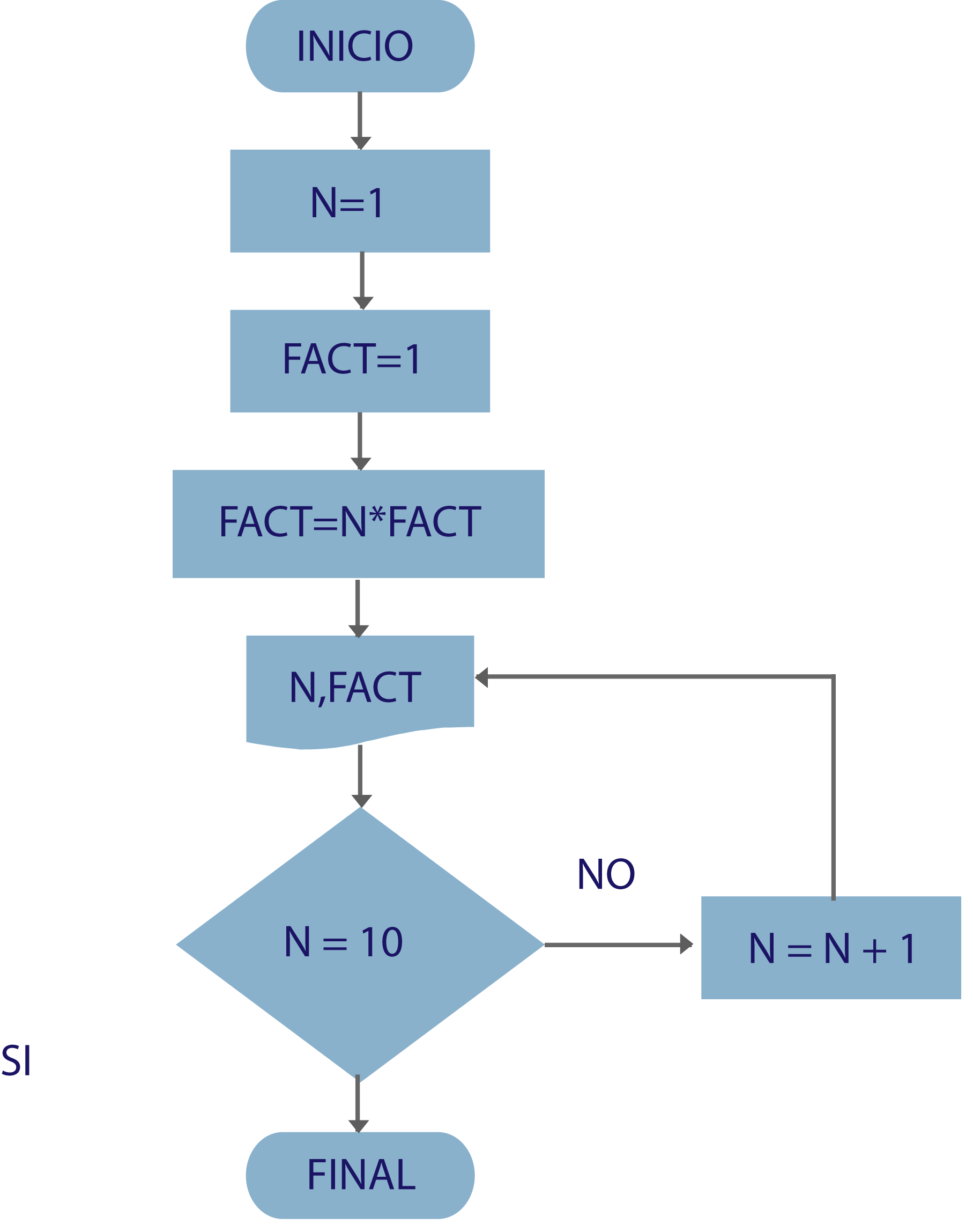
En el momento que se nos presenta un problema tratamos de solucionarlo lo más pronto posible, estudiando sus causas para actuar correctamente, tomando en cuenta que un algoritmo es una serie de pasos bien definidos que ayudan a llegar a la solución de algún problema. Es así como, mediante las diferentes técnicas de diseño de algoritmos, construimos soluciones que satisfagan los requerimientos del problema. Por eso la importancia de este tema, para identificar eficazmente todos los elementos posibles y así dar un resultado óptimo.
Si te interesa continuar con el tema te invito a seguir estudiando.
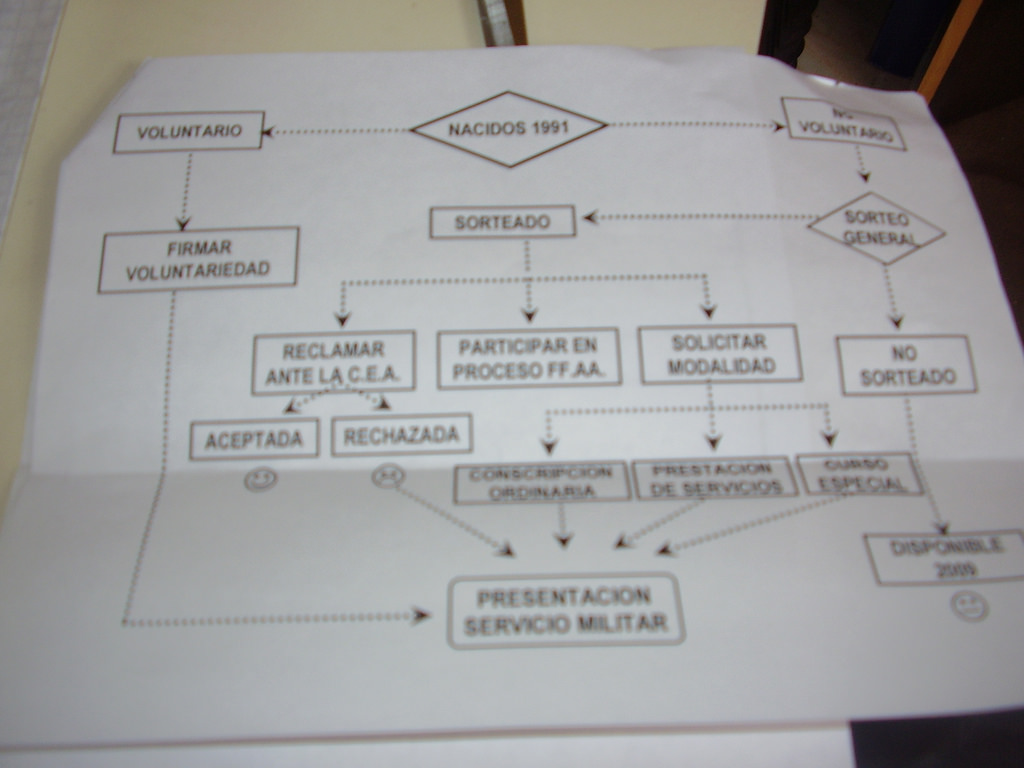
Geralt. (s. f.). Diagrama de flujo [fotografía]. Tomada de https://pixabay.com/es/marca-marcador-mano-deja-516277/