Derivada

Derivada

Iniciar

Introducción

¿Cómo evaluar el cambio? La derivada es una herramienta matemática para ello. Isaac Newton desarrolló los principios del cálculo diferencial en su obra Methodus Fluxiorum et Serierum Infinitorum (1671). En ese trabajo, da los pasos precisos alrededor de los conceptos de función y de límite, que le permiten plantear matemáticamente cuando las cantidades varían infinitesimalmente y, de esta forma, describir el movimiento de un punto que traza una curva, situación que expresa de la siguiente forma:

Por última proporción de cantidades evanescentes debemos entender el cociente de estas cantidades, no antes de que desvanezcan, ni después, pero tal como se van desvaneciendo. La parte infinitesimal pequeña en la que un fluente se incrementa por unidad de tiempo cero es el momento del fluente.



Representación de crisis global financiera

Idsoe, C. (2008). Solving the global financial crisis [fotografía]. Tomado de https://www.flickr.com/photos/cidsoe/3062812611/

El estudio de este tema te permitirá:

Aplicar el concepto de derivada en el análisis de problemas de valores máximos y mínimos, por medio de la derivación de funciones, utilizando el método de los cuatro pasos o las reglas de derivación, para la aplicación recurrente de este procedimiento que provee de otras herramientas de análisis matemático, útiles para determinar distintos comportamientos en la evolución de diferentes funciones.

Análisis del planteamiento de Isaac Newton


El texto reseñado puede analizarse en dos partes; la primera habla de cantidades evanescentes, es decir que se desvanecen o tienden a ser infinitamente pequeñas. Esto se puede contrastar directamente de la definición de límite: “[...] se dice que ‘L’ es el límite de la función ‘f(x)’ cuando la variable ‘x’ tiende al valor ‘a’ si la diferencia entre ‘f(x)’ y ‘(L)’ puede hacerse tan pequeña como se desee…”. En un cociente de cantidades con estas características, completa el texto.

Mientras la segunda parte habla de una parte infinitesimalmente pequeña que incrementa las variables (el fluente indica la letra) por unidad de tiempo.

Una vez extraídos estos elementos, se deben regresar al contexto sobre el que Newton trabajaba (el movimiento de una partícula), lo cual se ilustra a continuación:


Representación gráfica del movimiento de una partícula

Movimiento de una partícula en un tiempo inicial “x”, incrementado en una cantidad “∆” que es infinitesimalmente pequeña, esto es, x +∆; asimismo la función “f(x)” con la que se relaciona y su correspondiente incremento, f(x + ∆), a partir del trabajo sobre el movimiento de una partícula de Isaac Newton


En este escenario se observa que, sobre la curva descrita por el movimiento, hay un par de puntos y una diferencia entre estas posiciones en una proporción de cantidades que se hace cada vez más pequeña (evanescentes tanto como se desee, según el concepto de límite) por unidad de tiempo; a partir de esta discusión, se puede plantear la ecuación que describe esa acción de movimiento:




>

Al observar la ecuación (1), destaca la diferencia entre las posiciones (no en vano el término cálculo diferencial) con la parte infinitesimal en que se incrementa, numerador, tiempo (unidad de tiempo) y su correspondiente incremento en el denominador. El significado de la ecuación (1), según lo que ya conoces sobre el tema de funciones, es que ésta corresponde con la pendiente de la recta definida por los dos puntos del movimiento estudiado por Newton; de esta manera, se observa la formación de una recta secante (por definición, que corta a la curva en dos puntos) y se puede interpretar como se muestra a continuación:


Representación gráfica de la ecuación 1

La relación planteada por Newton es equivalente a la pendiente “m” de la recta secante que une dos puntos analizados en el movimiento estudiado


Adicionalmente a la interpretación matemática de pendiente, se tiene que en física esta misma relación define la velocidad promedio a que se mueve un objeto en la trayectoria planteada (cambio de posición entre tiempo). Pero ahora es interesante continuar con la propuesta de Newton: hacer que “∆” sea infinitesimalmente pequeña. Esto tiene dos implicaciones; la primera es que, al acercarse así, f(x + ∆) y f(x), la recta cortará a la curva sólo en punto y se convertirá en una tangente (por definición) a la curva. La segunda implicación es que, al acercarse el tiempo dado por (x + ∆) y (x) en la misma condición, se tendrá ahora un instante. De esta forma, la propuesta de Newton plantea que su aproximación en el límite será la velocidad del móvil en un instante, esto es, velocidad instantánea. Dicho de otra forma, será posible describir el comportamiento del punto en movimiento punto a punto, instante a instante.

Resulta sorprendente el planteamiento obtenido, ya que es una herramienta de análisis que no se había logrado por otro medio. Al aplicar de manera conjunta los conceptos de función y límite, se llega a este nuevo concepto que matemáticamente se denomina derivada de una función, una nueva herramienta que acepta interpretaciones equivalentes para una variedad muy amplia de problemas y, a partir de la función que define el fenómeno, permite determinar la velocidad máxima a que un auto puede circular en una carretera, la concentración de una mezcla o las variaciones en la bolsa, esto es, un sinfín de posibilidades.


Representación gráfica de la derivación de una función.

Derivación de una función, planteamiento que relaciona los conceptos de velocidad (física) y velocidad instantánea (matemática) con los de secante y tangente (geometría)


Derivada de una función


Así como ahora fue posible decir (a partir de lo anteriormente discutido) que la derivada de una función representa la recta tangente a una curva y es una herramienta que permite evaluar la forma en que se presenta el cambio en una función, será fácil entender e incluso intuir el procedimiento para obtenerla.

Este método se denomina método de los cuatro pasos para obtener la derivada de una función, y consiste en sistematizar el procedimiento realizado anteriormente.


Método de los cuatro pasos

Dada una función “f(x)” (como dijo Newton, el problema fundamental es obtenerla), su derivada se obtiene al seguir los cuatro pasos que se detallan a continuación. Pulsa las flechas para avanzar y retroceder por la información.

1. Evaluar la función para un incremento de la variable independiente (∆x), esto es:

f(x + ∆x)    (3.1)


2. Realizar la diferencia entre la función incrementada y la función:

f(x + ∆x) – f(x)    (3.2)

3. Realizar el cociente entre esta diferencia y el incremento de la variable independiente (∆x):


4. Evaluar el límite cuando este incremento (∆x) tiende a cero:



A continuación, se presenta un breve ejemplo para consolidar el aprendizaje del procedimiento enunciado.

Ejemplo 1. Un nuevo producto de una empresa tiene un comportamiento comercial obtenido a partir de los reportes de las ventas desde su fecha de lanzamiento, de acuerdo con la siguiente función matemática:

f(x) = x2 - 2x + 2 (e1); la variable “x” representa el tiempo y “f(x)” la venta de productos.

Obtener el comportamiento de las ventas mensuales asociadas para el primero, segundo y tercer mes.

Solución

Como ya sabes, se debe partir de la función que describe las ventas; para resolver el planteamiento, se aplica el concepto de derivada a través de la obtención de su ecuación por el método de los cuatro pasos. Pulsa las flechas para avanzar y retroceder por la información.

Previous Next

De esta manera se llega a la ecuación (e1p4), la cual permite evaluar el cambio de las ventas del nuevo producto y decidir su viabilidad comercial. Si se realiza esto para cada mes (x=1, x=2 y x=3), se obtiene:


a) x=1; 2x – 2: 2(1) -2 = 0
b) x=2; 2x – 2: 2(2) -2 = 2
c) x=3; 2x – 2: 2(3) -2 = 4


Para obtener las ordenadas de los valores en que esto sucede, se sustituyen los valores de la variable “x” en la ecuación original (e1), y se obtiene la ordenada correspondiente:


y(x) = x2 - 2x + 2


x = 1; y(1) = (1)2 - 2(1) + 2 = 1; (1,1)
x = 2; y(2) = (2)2 - 2(2) + 2 = 2; (2,2)
x = 3; y(3) = (3)2 - 2(3) + 2 = 5; (3,5)

Esto se ilustra a continuación:

Representación gráfica de cambio de ventas a partir del ejemplo 1

Las coordenadas correspondientes a los meses “x” evaluados


Así es como se obtienen los resultados solicitados. A continuación, observarás lo que se debe hacer con ellos.

Aplicación e interpretación de la derivada


A partir del Ejemplo 1, hemos aplicado el método de los cuatro pasos para obtener la derivada y evaluar así la variación en las ventas del nuevo producto, ahora interpretemos nuestros resultados. Para ello trazamos la gráfica de nuestras ventas (equivalente al movimiento en el problema de Newton) y tracemos las tangentes indicadas (esa es su interpretación directa, ¿no?); retomándolas de los resultados del ejemplo uno, lo que ilustramos a continuación:


Representación de la gráfica de ventas a partir del ejemplo 1

Gráfica de las ventas, dada por la función (x2 - 2x + 2) en rojo; en colores azul, verde y café, las tangentes obtenidas por la evaluación de la derivada de la función (2x - 2). En este caso, la función de las ventas es aplicable a partir del mes cero, fecha del lanzamiento del producto, por ello se indican en línea punteada los valores previos


Los resultados obtenidos provienen de evaluar la derivada (2x - 2). Para el mes 1, x = 1, la derivada vale cero; mes 2, x = 2, la derivada vale 2; mes 3, x = 3, la derivada vale 4. No olvides que cada derivada representa la pendiente de la tangente en el mes correspondiente; al buscar responder lo que representa cada uno de estos valores, se puede investigar lo que indica la relación trigonométrica en inversa, es decir, se investiga el ángulo que genera ese valor. De esta forma:


tan-1(0) = 0 °; m = 0
tan-1(2) = 63.4 °; m = 2
tan-1(4) = 75.9 °; m = 4


Con base en que “tan-1(x)” permite conocer el ángulo para el cual se obtuvo el valor reportado, observa que cada tangente refiere una inclinación asociada (su pendiente) y, si cada una representa la variación de las ventas, es posible deducir a partir de la gráfica que, efectivamente, el primer mes no hubo un cambio en las ventas, en el segundo mes se incrementaron notablemente y en el tercero las ventas fueron un rotundo éxito.

¿Interpretaciones comerciales a estos resultados? ¿Una nueva planta? ¿Mayor promoción del producto? Las respuestas a estas preguntas dependen ahora del área de gerencia y mercadotecnia; desde esta área, lo que se hizo fue aportar los elementos para que ellos tomen las decisiones.

Notación de la derivada


Así como para cada operación aritmética y algebraica hay un símbolo asociado, por ejemplo en la suma (+), resta (-) y así sucesivamente, para la derivada también hay notación, pero no es única; esto se debe a que Newton no fue el único en investigar sobre el tema. Por ello, es posible encontrar otras notaciones utilizadas por los matemáticos que participaron en sus avances, lo cual vuelve necesario indicar la simbología que se puede encontrar en la bibliografía. Dicha simbología se muestra a continuación; pulsa cada una para conocer más al respecto.

Notación de Lagrange

f´(x); esto es una comilla asociada a la función    (1)


Notación de Leibniz

df/dx; un cociente como el propuesto por Newton    (2)

Notación de Cauchy

Dx; una “D” mayúscula denominada operador derivada en la variable “x”    (3)

Notación de Lagrange

Asimismo podemos indicar una más que se relaciona con la notación de Lagrange:

y´    (4)


Aunque se usan indistintamente, a lo largo del tema se utilizarán con mayor frecuencia las notaciones (1), (2) y (4).


Reglas para determinar la derivada de una función


El procedimiento para obtener la derivada de una función por el método de los cuatro pasos es directo; sin embargo, hay funciones donde realmente se llega a complicar el desarrollo algebraico y la determinación de los límites. Previamente conociste que es posible encontrar funciones de tipo algebraico, trigonométrico, exponencial y logarítmico, entre muchas otras.

Por ello, se han obtenido reglas que relacionan una función “tipo” con su derivada; las mismas se han obtenido a través de la aplicación del método de los cuatro pasos a ecuaciones de carácter general para su clase. A continuación, se enlista un conjunto breve de estas reglas para funciones algebraicas:




Algunas reglas para la derivación para funciones algebraicas. La aplicación requiere ajustar nuestra función a uno de los tipos indicados a la derecha


Con el fin de extender el acervo en este punto, se pueden consultar en la bibliografía matemática una variedad de tablas para ampliar a este tema. A continuación, se muestra un ejemplo:

Ejemplo 2. Con base en la función vista en el ejemplo 1 (x2 - 2x + 2), realizar su derivación a través de las reglas listadas.

Solución

Si se considera que la función (e1) es una suma de funciones, se aplican las pautas indicadas por las literales (c), (h - d), (b) y (a); esto se realiza de manera correspondiente en cada renglón y se ilustra a continuación:





Si observamos las ecuaciones (e2) y (e1p4) vistas anteriormente, se aprecia que el resultado de la derivación es idéntico, lo cual es normal ya que, si bien fueron obtenidas por diferente método de derivación, el resultado debe ser el mismo al tratarse de la misma ecuación. Dicho de otra forma, la derivada de una función es única.

Derivadas de orden superior


Si se considera que Newton desarrolló el cálculo diferencial a partir del estudio del movimiento de un punto en una curva, y éste se interpretaba como la velocidad del punto en movimiento, es posible pensar si así cambia la posición (indicada por la velocidad). ¿Cómo cambia la velocidad misma?

Los elementos para contestar esta pregunta sin mucho problema ya se tienen a la mano; uno es la derivación, la cual puede informar sobre la manera en que sucede esto. El hecho de derivar una función sucesivamente se denomina derivación de orden superior; el algoritmo para realizarla es el mismo y la notación de esta acción es similar. En el estilo de Lagrange es fácil indicarla, ya que es recurrente en su escritura:

y´      (primera derivada)
y´´    (segunda derivada)
yn      (enésima derivada)


El interés de realizar derivaciones de orden superior se debe a que la derivada es una herramienta matemática muy versátil para evaluar el cambio en una función, y su aplicación depende mucho de las interpretaciones que se hagan de sus resultados.

Ejemplo 3. Con base en los resultados del ejemplo 2, determinar la segunda derivada de la siguiente ecuación:

2x - 2

Solución

Al aplicar las reglas de derivación asociadas a los incisos (c), (d), (a) y (b), se muestra el resultado:





El resultado indicado por (e3) señala que el cambio en las ventas se mantendrá constante, lo cual se interpreta así: mientras no haya algún ajuste en la competencia y la mercadotecnia, el producto se mantendrá en su línea de demanda.

Cabe mencionar que ahora la problemática no es el uso de la herramienta, sino la correcta interpretación de los resultados.


Derivada y valores máximos y mínimos de una función


A lo largo del tema se ha recalcado que la derivación de funciones provee una herramienta matemática muy poderosa; en esta línea, se muestra una metodología asociada a su aplicación que permitirá encontrar los valores máximos y mínimos de la función. ¿Cómo realizar esto? La forma de hacerlo tiene que ver con la propia interpretación geométrica de la derivada; para ilustrarlo, se muestra nuevamente la gráfica de la función de las ventas del ejemplo 1.


Representación de la gráfica de la ecuación x<sup>2</sup> - 2x + 2

Gráfica de la ecuación x2 - 2x + 2


¿Qué observas de esta gráfica respecto a los valores máximos o mínimos para las ventas de nuestro producto?


Evidentemente se distingue que, en ella, hay un valor mínimo (no así un máximo en este caso, pues la función es creciente). ¿De qué manera puede la derivación brindar información al respecto? La respuesta se obtiene al presentar la evaluación de la derivada para tres diferentes momentos alrededor de este valor mínimo. Se evalúa entonces la derivada para medio mes (x = ½), para un mes (x =1) y para mes y medio (x = 1½), y luego se analizan los resultados:

a) x = ½; 2x – 2 = 2(½) – 2 = 1 – 2 = -1
b) x = 1; 2x – 2 = 2(1) – 2 = 0
c) x = 1½; 2x – 2 = 2(1½) – 2 = 3 - 2 = 1


Representación gráfica de las pendientes de las tangentes

Pendientes de las tangentes m = -1 para x = 0.5; m = 0 para x = 1; m = 1 para x = 1.5


Si ahora se obtienen los valores de los ángulos para los cuales se presentan estos valores, se tiene lo siguiente:

a) tan-1(-1) = -45°
b) tan-1(0) = 0°
c) tan-1(1) = 45°


Al observar estos resultados se aprecia que, antes del valor mínimo de la ecuación de las ventas, el ángulo es negativo, en el punto mínimo es 0° y, en la parte creciente, el ángulo es positivo. Se concluye entonces que, al presentarse un mínimo en una función, esto debe darse de forma que el cambio en la pendiente de la tangente (derivada) vaya de menos a más (grados) pasando obviamente por 0°.

En esencia, es una metodología que puede ayudar a ubicar estos valores mínimos, y también máximos, como veremos en el siguiente ejemplo.

Derivada y valores máximos y mínimos de una función


Ejemplo 4. Encontrar los valores máximos que se presentan en la siguiente ecuación:

–x2 + 4x -2

Solución

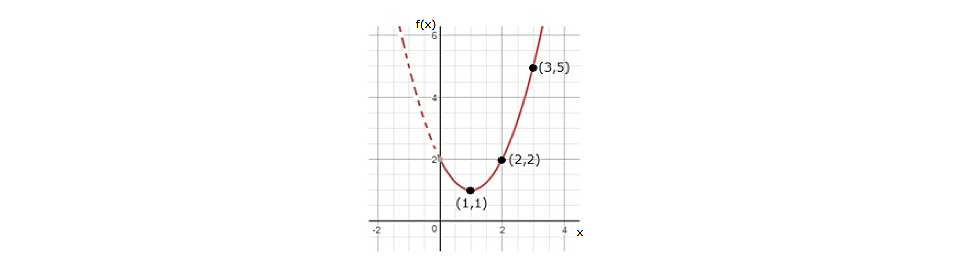
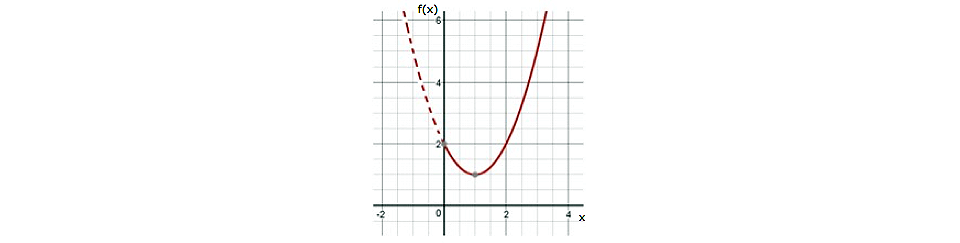
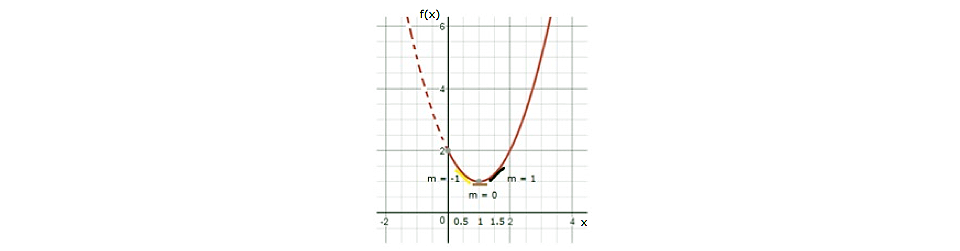
Antes de realizar el desarrollo, se muestra la gráfica asociada a dicha ecuación:


Gráfica de la ecuación –x2 + 4x - 2 en el intervalo x(0,4)

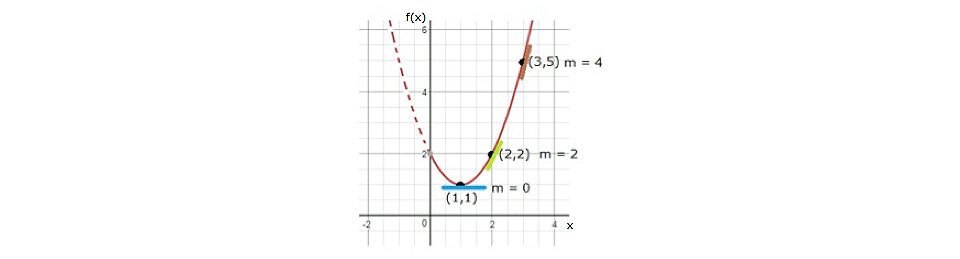
Gráfica de la ecuación –x2 + 4x - 2 en el intervalo x(0,4)


Al observar nuestra gráfica se aprecia que, a diferencia del ejemplo sobre los mínimos, ésta tiene un valor máximo en la coordenada (2,2); entonces, igual que en aquel caso, se obtiene la derivación y se realiza una evaluación alrededor del punto máximo.

Derivación:



La ecuación (e4) se anula para x = 2; al observar los puntos alrededor de este valor, se toman lateralmente las abscisas x = 1 y x = 3 y se evalúan en (e4):

a) x = 1; -2(1) + 4 = -2 + 4 = 2
b) x = 2; -2(2) + 4 = 4 – 4 = 0
c) x = 3; -2(3) + 4 = -6 + 4 = -2

Representación gráfica de las pendientes de las tangentes m = 2 para x = 1; m = 0 para x = 2; m = -2 para x = 3

Pendientes de las tangentes m = 2 para x = 1; m = 0 para x = 2; m = -2 para x = 3


Al obtener los ángulos correspondientes:

a) tan-1(6) = 63.43°
b) tan-1(0) = 0°
c) tan-1(-2) = -63.43°

Nuevamente se observa un cambio de signos alrededor del punto donde se presenta el máximo; sin embargo, al observar con más cuidado, se aprecia que ahora se da en sentido contrario (positivo, cero, negativo).

De esta manera, es posible resumir la forma en que se puede determinar cuándo se presenta un máximo y cuándo un mínimo a través de la derivación de dicha ecuación.

1. Obtener la derivada de la función bajo análisis, igualar dicha ecuación a cero y obtener las soluciones para esa condición.
2. Evaluar para valores cercanos antes y después de esos puntos donde se anula la derivada.
3. Obtener, si se presentan, los cambios de signo asociados a las tangentes evaluadas.
4. Se presenta un máximo si la variación de signos alrededor del valor que se anula se da de esta forma: positivo-cero-negativo.
5. Se presenta un mínimo si la variación de signos alrededor del punto que se anula se da de esta manera: negativo-cero-positivo.


Esto se resume en la siguiente tabla:

Posición relativa Variación de los signos de la primera derivada
Máximo + 0 -
Mínimo - 0 +

Tabla 1. Determinación de máximos y mínimos de una función, a partir de los valores de “x”, donde se anula su primera derivada


Para finalizar, no hace falta obtener el valor del ángulo (tan -1), ya que el cambio de signos se observa desde antes; esto se realizó como una estrategia que aclarara aún más la interpretación de la pendiente de la tangente asociada.

Conclusión


El cálculo diferencial inventado por Newton se ha convertido en una poderosa herramienta matemática del mundo actual, ya que abre el camino para evaluar el cambio, lo cual es pieza fundamental de muchas ciencias. Los conceptos de función, límite y derivada son su soporte y se entretejen finamente; por ello, es necesario tener una visión completa alrededor de ellos para contar con mejores elementos que permitan realizar la interpretación de los resultados de los problemas abordados.




Zanarini, P. (2010). Netflix: $50-> $100 in 3 months! [fotografía].
Tomada de https://www.flickr.com/photos/zipckr/4554086740/




(s. a.) (2007). Nasdaq Take 5 [fotografía].
Tomada de https://www.flickr.com/photos/bfishadow/3100371688




Bramley, B. (1992). GodfreyKneller-IsaacNewton-1689 [pintura].
Tomada de https://commons.wikimedia.org/wiki/File:GodfreyKneller-IsaacNewton-1689.jpg


Los datos del índice bursátil brindan los elementos para construir la función que describe su comportamiento, mientras la derivación permite evaluar cómo se da el cambio en función de sus variables.

Actividad de aprendizaje. Punto de inflexión y derivadas de orden superior

La derivada es una herramienta versátil que acepta diversas interpretaciones; así como es posible determinar la pendiente de la tangente en un punto de una curva, también se pueden hallar los valores máximos y mínimos de una función y ubicar a través de ella las concavidades de una función.

Para el desarrollo de esta actividad considere la siguiente ecuación:

f(x) = x3 + 2x2      (1)

A partir de la ecuación planteada, lee las siguientes aseveraciones y responde si son verdaderas o falsas. Para ello, pulsa el alveolo correspondiente; al terminar, podrás conocer tu desempeño.


Autoevaluación. Derivada una herramienta matemática para evaluar el cambio

En el pasado, dar respuesta a la evolución de una función matemática era imposible; ahí reside la importancia de la derivación de funciones. Con esta herramienta de análisis, es posible encontrar los valores y las condiciones en que se presentan las variaciones, lo cual ayuda a prever y enfrentar las situaciones asociadas a estos cambios.

Revisa los siguientes enunciados y elige la opción que complete correctamente cada uno. Al terminar, podrás conocer tu desempeño.

Fuentes de información

Básicas

Bibliografía


Ayres, F. (1980). Cálculo Diferencial e Integral. México: McGraw-Hill.

Granville, W. (1963). Cálculo Diferencial e Integral. México: Unión Tipográfica Editorial Hispano-Americana.


Sitios electrónicos


DGTIC-UNAM (2013). Sección: Definición de la derivada y sus diferentes notaciones. Consultado el 24 de noviembre de 2017 de http://www.objetos.unam.mx/matematicas/leccionesMatematicas/03/3_019/index.html


Complementarias

Bibliografía

Luthe, R. (1984). Métodos Numéricos. México: Limusa.


Cómo citar