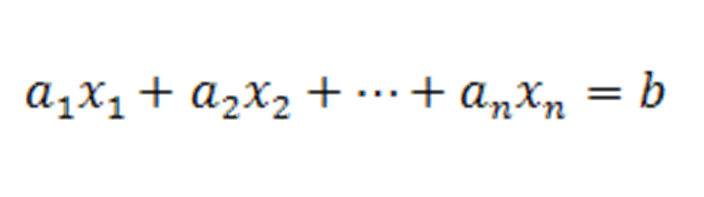Vectores y matrices
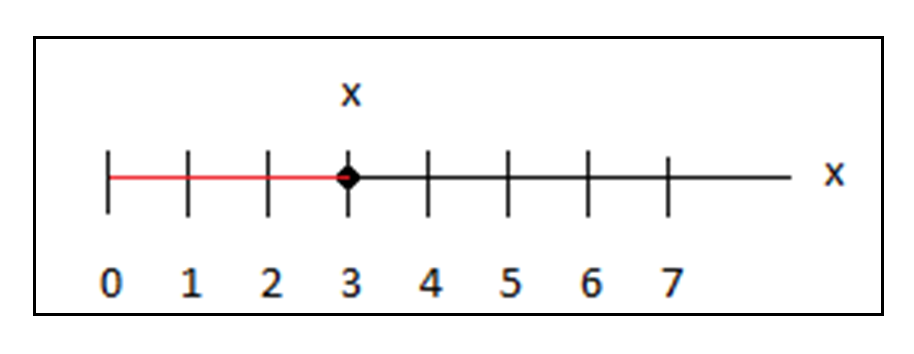
A través de un número (x), esta recta define una ubicación única en la recta.
Ejemplo de pareja ordenada de números.
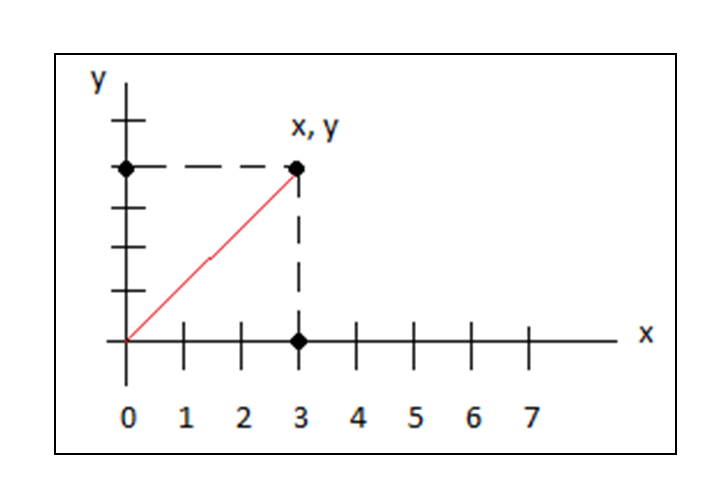
En el plano cartesiano se requiereuna pareja ordenada de números (x,y) para determinar una ubicación específica en una superficie.
Pareja ordenada de números
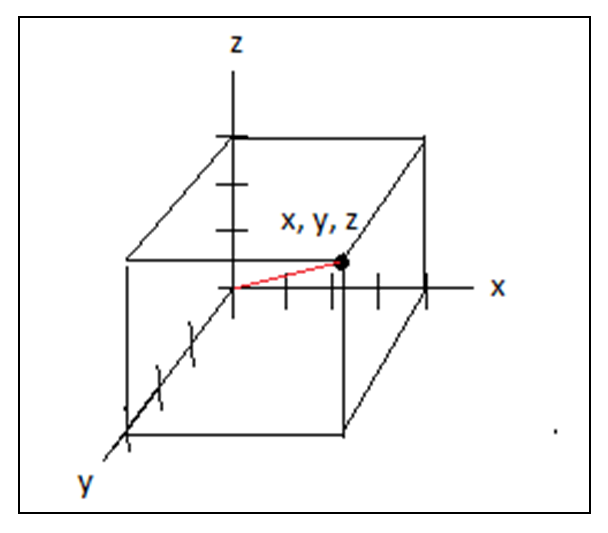
En el espacio tridimensional, se necesita una terna ordenada de números (x,y,z) para determinar la posición de un punto en el espacio.
Terna ordenada de números
A partir de estos escenarios, se observó la posibilidad de enfrentar problemas donde ya no hay un equivalente físico o geométrico, para los cuales se construyeron los conceptos de estructuras o espacios vectoriales. La base de ellos es el vector, el cual es un grupo de valores ordenados, distinguidos como n-tuplas, a partir de los cuales se puede determinar otro valor de manera unívoca; su notación se muestra a continuación:
En estas estructuras meramente matemáticas, se relacionan de manera simultánea las variables independientes (a1, a2,…, an) con otro valor dependiente de ellas (v). Sin embargo, las nuevas estructuras matemáticas mantienen cierta similitud con modelos anteriormente desarrollados para problemas de menos variable, como la ecuación de una recta como la que se muestra a continuación:
En ella se observa una variable libre, en este caso “x”, con una variable dependiente “y”; los vectores también pueden relacionarse con otros vectores y tener configuraciones denominadas sistemas de ecuaciones que simultáneamente requieren satisfacerse. Esto se denota de la siguiente forma:
Estas nuevas ecuaciones requieren la creación de un lenguaje y una estructura matemática de soporte que permita desarrollar métodos para trabajar con estos entes abstractos. Bajo estos arreglos, el grupo de variables independientes {(a1, a2,…, an), (b1, b2, …, bn) … (m1, m2, …, mn)} puede descomponerse a través de un proceso multiplicativo en dos elementos separados para establecer una estructura parecida a la presentada en la ecuación (a) y, por medio de esto, volver a expresar la ecuación (b) como se muestra a continuación:
Al grupo ordenado de elementos (d1, d2, …p1...pn), distribuido como un arreglo de renglones-columnas y colocado entre corchetes, se le denomina matriz de coeficientes, en tanto los grupos ordenados por columna (x1,x2…xn) y (v,u,…z) se denominan vector independiente y vector dependiente, respectivamente; por razones obvias, a la ecuación (c) se le conoce también como ecuación matricial lineal y se denota con la siguiente ecuación:
Donde “A” representa a la matriz de coeficientes (d1, d2, …p1...pn) y “x” y “y” representan en ese orden a los vectores independiente y dependiente.
Es importante resaltar las características “mxn” (renglones-columnas) de una matriz o vector, ya que a partir de éstas será posible realizar operaciones matemáticas entre ellos. A diferencia de los números reales, a los que siempre es posible sumarlos, restarlos o multiplicarlos, en el caso de las operaciones entre matrices o matriz-vector debe verificarse previamente su compatibilidad.
La compatibilidad se determina de la siguiente manera:
Swipe left or right
Para la operación de suma, se requiere que el parámetro renglón columna “mxn” (también conocido como orden de la matriz o vector) de ambos elementos a sumar sean idénticos.
Owen-Wahl, R. (2006). Pluma, regla y calculadora [fotografía]. Tomada de https://pixabay.com/es/%C3%A1lgebra-analizar-arquitecto-1238600/
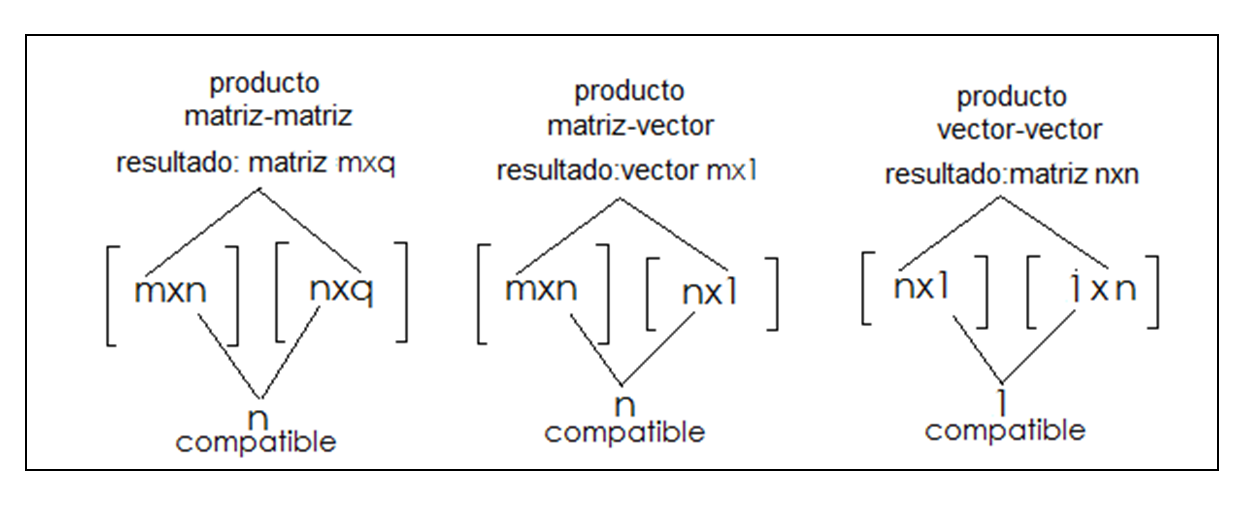
En el caso de la multiplicación, la compatibilidad renglón-columna se verifica de la siguiente forma: para que una matriz de coeficientes de orden “mxn” se pueda multiplicar con otra matriz o vector, cualquiera de estos debe tener un orden “nxq” (matriz) o “nx1” (vector) de tal forma que, al colocarlos en el orden indicado por la multiplicación, las literales que describen los renglones y columnas (o sus correspondientes números) contiguos deben ser iguales, en tanto que el orden renglones-columnas del resultado de la operación lo proporcionan las literales (o números) no contiguos. Esto se muestra a continuación:
Previous Next
Un ejemplo de multiplicación entre una matriz de coeficientes “3x3” y un vector independiente “3x1” dan como resultado un vector dependiente “3x1”, como se muestra a continuación:
Orden de la matriz
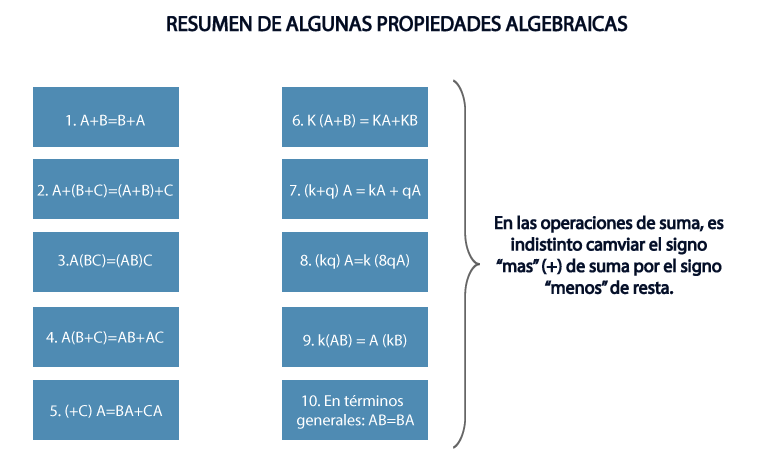
En el siguiente cuadro, se muestran algunas propiedades; se toma en cuenta que “A”, “B” y “C” son matrices y “k” y “q” son escalares.
Ejemplo de propiedades algebraicas
A continuación, se muestra una nomenclatura muy utilizada de vectores y matrices, así como algunas propiedades algebraicas adicionales.