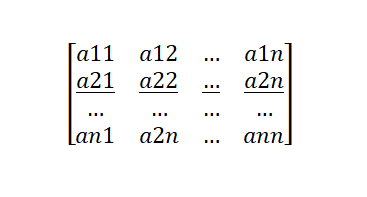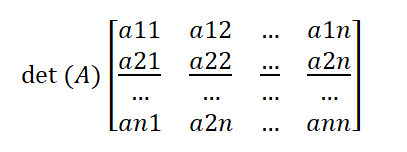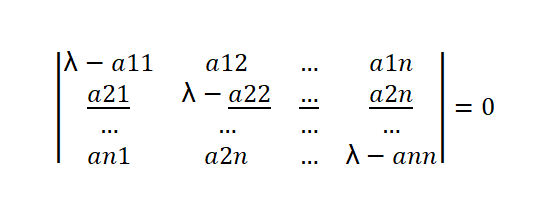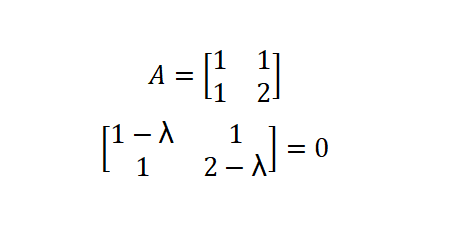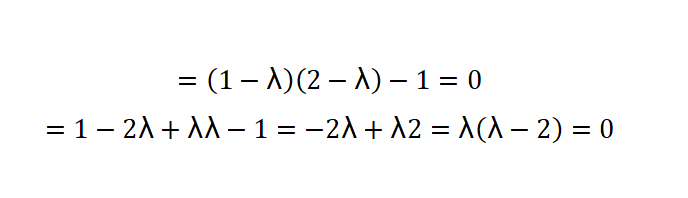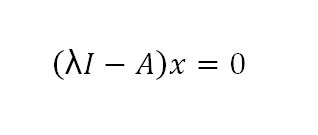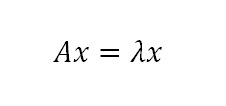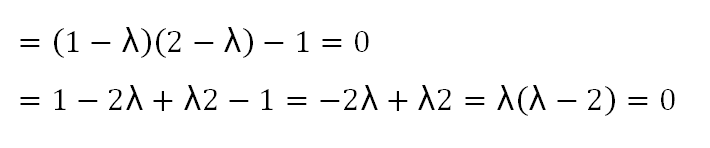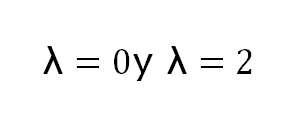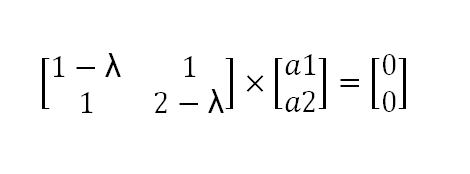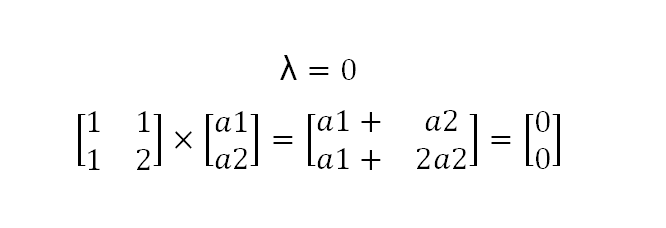Introducción
En la actualidad, los requerimientos analíticos de las empresas avanzan rápidamente; por este motivo, se requieren modelos y algoritmos más complejos para la solución de los problemas.
Para determinar y resolver las interacciones que generen mejores procesos productivos y rindan mayores utilidades para las organizaciones es menester construir complejos modelos en los que se interrelacionan sistemas de ecuaciones y transformaciones lineales; es indispensable, entonces, conocer una variedad de herramientas que nos permitan plantear, analizar y resolver estas estructuras de manera rápida, con un cierto nivel de versatilidad y que, además, se adapten a las condiciones cambiantes de los negocios.
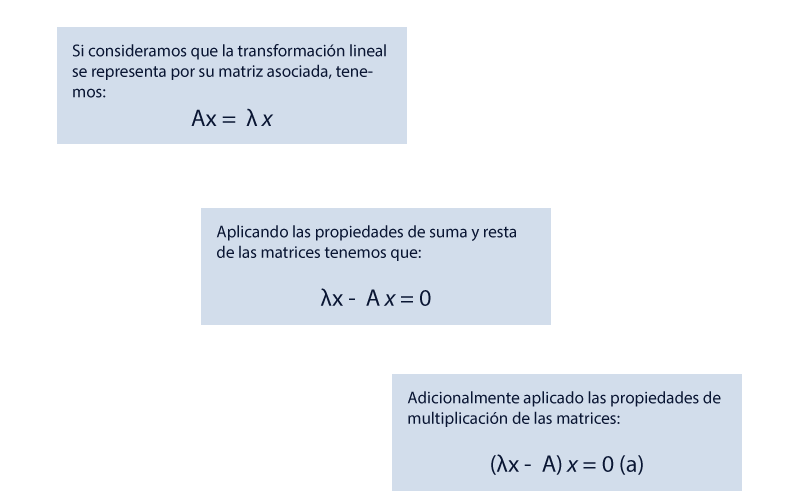
Es en estos entornos donde los conceptos de determinante, valores y vectores característicos encuentran un importante nicho de aplicación; por tanto, es de suma importancia conocer y dominar las técnicas matemáticas avanzadas que nos ofrece el álgebra lineal en diversos campos del conocimiento, de los cuales destaca el de la informática.