Método de ordenación por intercambio
Imagina que de un conjunto de datos o elementos introduces y aíslas dos de ellos en una burbuja inteligente, como si fueran los únicos en el mundo. La burbuja descubre cuál de los dos elementos es mayor y los intercambia, si es necesario; de manera que deja al menor del lado izquierdo y al mayor del lado derecho.
Con la microoperación explicada anteriormente, nuestra burbuja inteligente sólo ordenó dos elementos, de menor a mayor; sin embargo, dicha operación puede aplicarse varias veces (sobre un arreglo o lista de elementos) hasta dejar todos los elementos ordenados.
El ordenamiento por intercambio o bubble sort funciona de la siguiente manera:
En relación a lo anterior, podemos decir que el algoritmo bubble sort consiste en comparar pares de elementos adyacentes e intercambiarlos entre sí hasta que estén todos ordenados; este método también es conocido como intercambio directo.
Ejemplo:
Sea un arreglo de seis números de empleados:
La complejidad de este algoritmo es de O(n2), donde n es el número de elementos del arreglo o lista.
Primera pasada:
Como puedes ver, el elemento mayor siempre es llevado hasta el final del arreglo en cada pasada.
Segunda pasada:
Ya están ordenados, pero para comprobarlo habría que acabar esta segunda vuelta y hacer una tercera en la que veremos que no hubo intercambios, y de esa manera sabremos que el arreglo ya está ordenado.
Para su implementación, generalmente, definimos una función donde:
Observa la siguiente imagen:
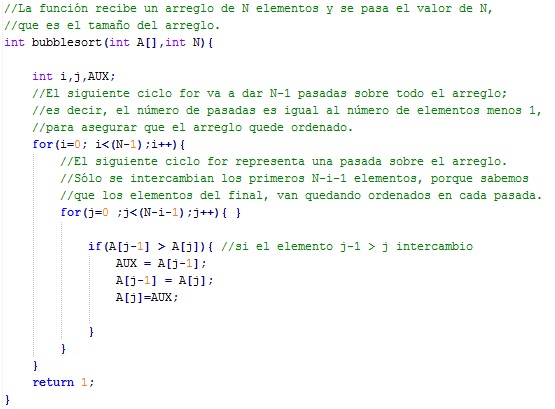
Declaración de la función de ordenamiento por bubble sort.
En la declaración de código anterior de la función bubble sort utilizamos dos ciclos for anidados con los índices i y j para ir comparando y ordenando los elementos durante el recorrido del arreglo.
Como puedes observar, en la implementación dimos N vueltas al arreglo, pero la implementación se puede mejorar si cada vez que das una vuelta compruebas si el arreglo ya está ordenado; en ese caso ya no se darán más vueltas y se da por terminado el ordenamiento.
Haciendo el análisis de eficiencia de este método, podemos ver que es el más fácil de implementar; sin embargo, si se cuenta con un mayor volumen de datos se vuelve ineficiente; ése es un rasgo que te permitirá saber si será el correcto a utilizar o no.
Así pues, partiendo de un número (n) de elementos, en el método bubble sort tendremos comparaciones consecutivas entre pares de números, de tal manera que:
•En la primera pasada tendremos (N-1) comparaciones.
•En la segunda (N-2).
•Así sucesivamente hasta llegar a 2 y 1 comparaciones entre elementos, dependiendo de tamaño del arreglo.
|
Por lo anterior, podemos ver que no es un algoritmo recomendado para una gran cantidad de elementos, ya que, en promedio, y en el peor de los casos, su complejidad es O(nn) y en el mejor de los casos es O(n); donde n es el número de elementos a ordenar.

