Introducción
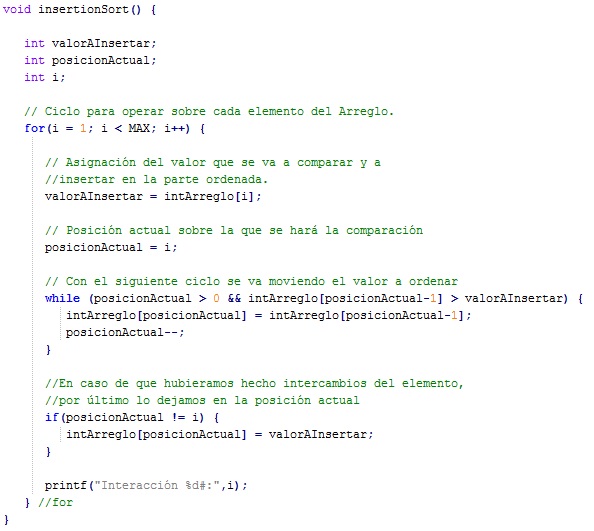
Imagina que tienes una baraja dividida en dos partes; una mitad está ordenada y la otra está desordena, después, tomas las cartas de la mitad desordenada y las insertas una por una, de manera ordenada, en la otra mitad de manera que dicha mitad no pierda la característica de ser la ordenada. Ésta es la forma, a grandes rasgos de cómo funciona el método de ordenamiento por inserción directa.
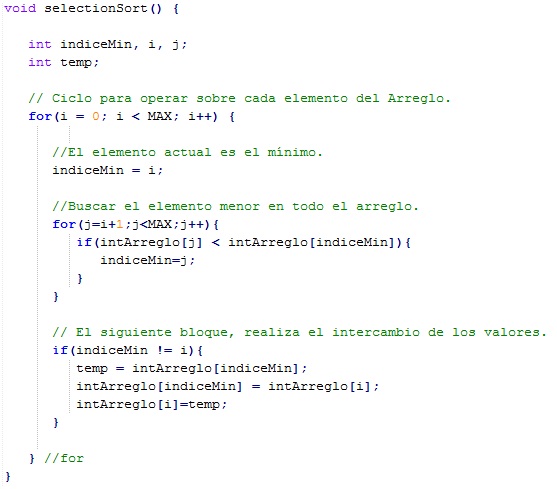
Ahora imagina que tenemos una baraja, vamos a utilizar otra estrategia para lograr nuestro objetivo de ordenarla. Lo que hacemos es dividir el juego en dos partes, la parte ordenada quedará del lado izquierdo y la parte sin ordenar quedará del lado derecho; en un inicio, del lado izquierdo no hay nada, porque la parte ordenada está vacía. Luego nos vamos al juego de cartas y seleccionamos el elemento de menor valor de una sola figura, es decir; el dos (recuerda que en una baraja no hay uno ni cero), ese elemento se pone del lado izquierdo en la parte ordenada y así sucesivamente hasta que tengas toda la baraja ordenada del lado izquierdo. Ésta es la forma, a grandes rasgos, en que funciona el ordenamiento por selección.

Analogía de ordenamiento por selección