Introducción
En la práctica profesional es habitual enfrentar situaciones donde se requiere apoyar o no un supuesto sobre el comportamiento de una distribución. Por ejemplo, al área de mercadotecnia de una empresa de cosméticos le gustaría comprobar si el 75% de las mujeres entre 30 y 40 años que laboran utilizan un labial de color café.
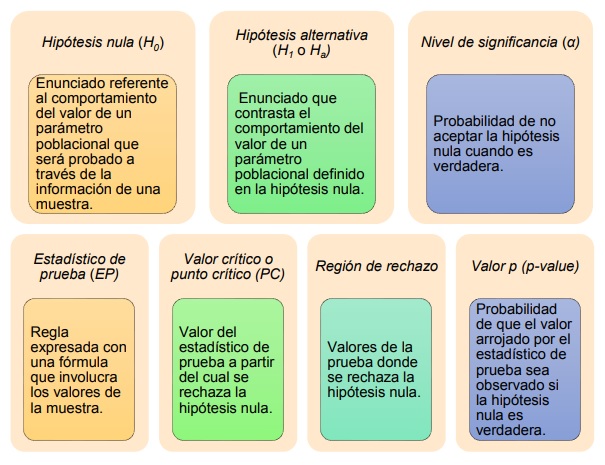
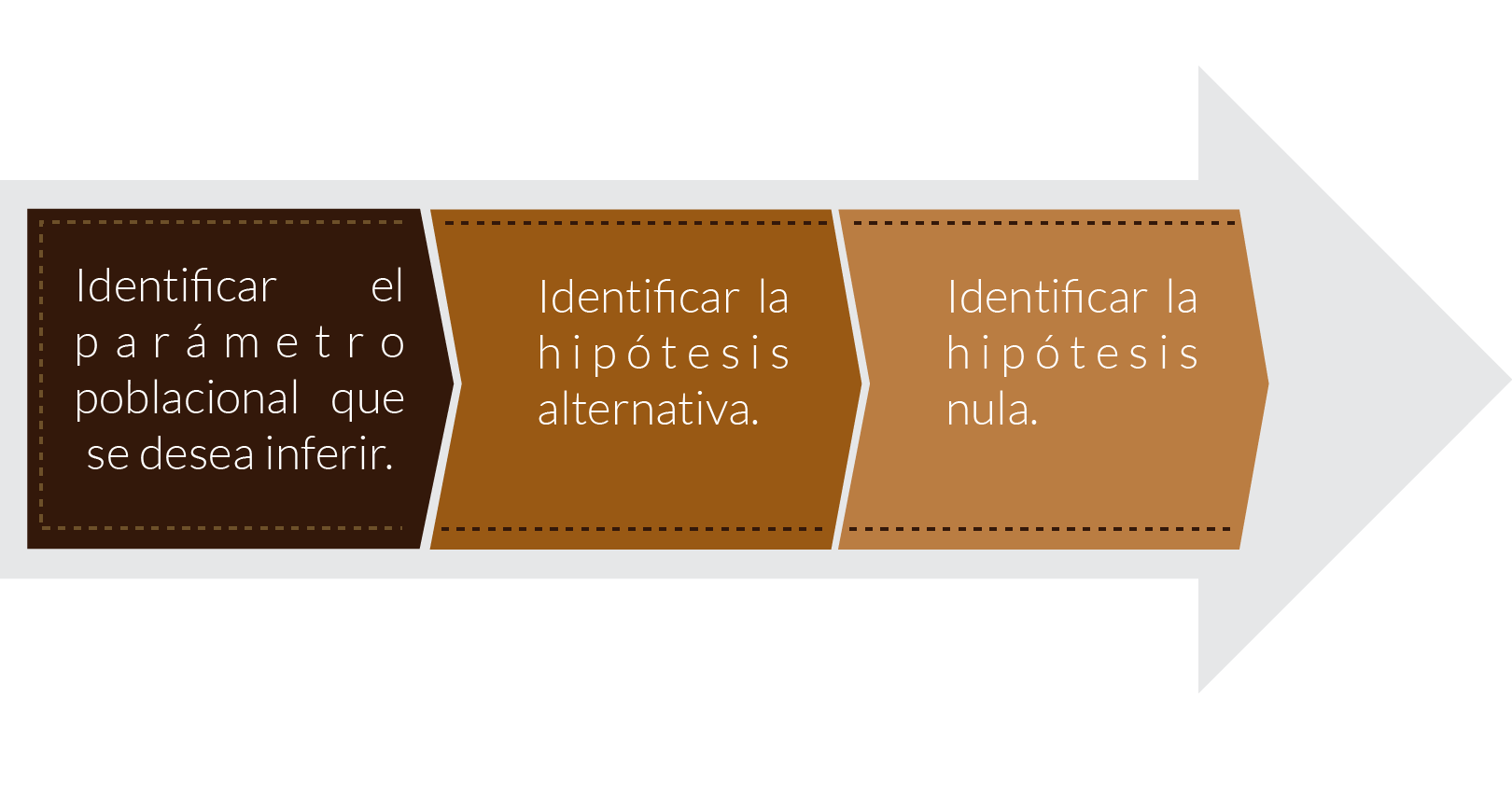
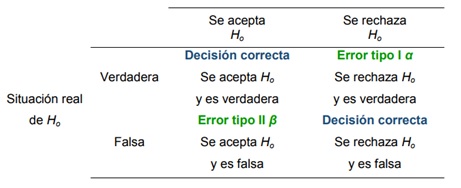
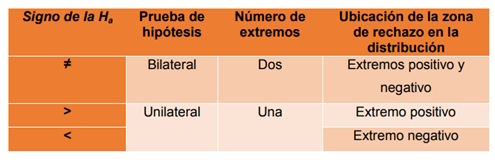
Para ello se utilizan las hipótesis y en este tema se abordarán las partes que las componen y cómo plantearlas; además, se explican los tipos de errores que se pueden cometer al momento de definir una prueba de hipótesis.
¡Comencemos!

Schweiz, A. (2016). Cosméticos [fotografía]. Tomada de https://pixabay.com/es/cosm%C3%A9ticos-l%C3%A1piz-labial-1367782/