Estadística Inferencial: Muestreo Aleatorio Simple

Unidad de Apoyo para el Aprendizaje

Iniciar

Introducción


Las organizaciones constantemente analizan sus productos y servicios, y miden la forma en cómo sus clientes se benefician de éstos.

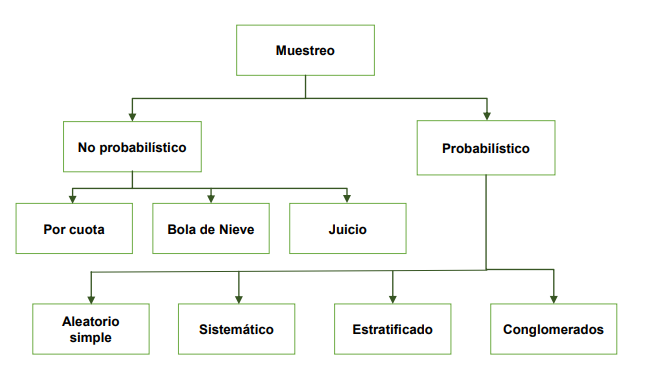
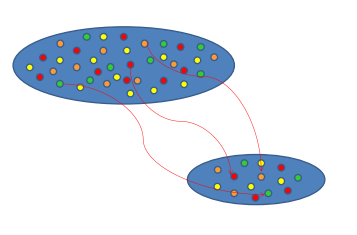
Para ello, recurren a diferentes tipos de muestreo con el propósito de identificar tamaños de muestra de una población, siempre cuidando que éstos sean representativos. El muestreo en el que nos centraremos es el aleatorio simple.

A continuación se expondrá la importancia del error de estimación, la metodología del muestreo aleatorio simple y el cálculo de tamaño de muestra, a partir de diferentes casos prácticos.

¡Comencemos!



satisfacción del cliente.

(s. a.) (2017). Satisfacción [ilustración]. Tomada de https://pixabay.com/es/comentarios-examen-opini%C3%B3n-1978036/

El estudio de este tema te permitirá:

Identificar las características de la metodología de muestreo aleatorio simple, a partir de la revisión de diferentes ejemplos, para la estimación de una media y proporción poblacional.

Muestreo y error de estimación


Al momento de calcular el tamaño de una muestra, son muchas las metodologías que podemos utilizar, ya sea muestreo probabilístico también llamado aleatorio, y muestreo no probabilístico o conocido como de juicio.


Muestreo


Rodríguez, A. y García, M. (2012). Principales tipos de muestreo aleatorio (probabilístico) y de juicio (no probabilístico) [imagen]. Tomada de Estadística II [Versión electrónica].




Se debe tener presente que en todo ejercicio de muestreo no se está recabando información de toda la población, por lo que va a existir un error de estimación y, de antemano, debe fijarse el límite de error permitido.

El arte del muestreo consiste en determinar la muestra que minimice ese error. Cuando se recaba información de una muestra, se pueden presentar dos tipos de errores:

Atribuibles al muestreo No atribuibles al muestreo
Son por la diferencia entre el valor del estimador muestral y el valor del parámetro poblacional, considerando la información de la muestra con la que se trabajó. Se explican, entre otras causas, por un mal diseño del instrumento, la logística implementada o una elevada tasa de no respuesta.

Para lograr lo anterior, el tamaño de muestra juega un papel central, ya que a medida que se tenga más información de un parámetro, se incrementa la probabilidad de realizar una estimación certera.

Muestreo aleatorio simple


En este método, las unidades de población tienen la misma probabilidad de ser elegidas, porque cada elemento es seleccionado aleatoriamente. En la siguiente figura se ilustra cómo funciona esta metodología:

muestra extraída de la población


Rodríguez, A. y García, M. (2012). Funcionamiento del muestreo aleatorio simple [imagen]. Tomada de Estadística II [Versión electrónica].



El óvalo de mayor tamaño representa la población de interés; y los puntos contenidos, las unidades muestrales. En tanto, el óvalo de menor tamaño simboliza la muestra extraída de la población.

Las flechas indican que las unidades muestrales contenidas en la muestra provienen de la población, su elección se realizó de manera aleatoria. Por ejemplo, en la comida de fin de año de una empresa, se realiza una rifa con 20 premios, se meten todos los nombres de los empleados en una tómbola y se van extrayendo los ganadores, uno a uno, de forma aleatoria.

En la siguiente tabla se exponen las fórmulas para calcular el tamaño de una muestra, para estimar una media y una proporción (parámetros) cuando se tiene conocimiento del tamaño de la población N y cuando no es así.

Fórmulas


Rodríguez, A. y García, M. (2012). Fórmulas para calcular el tamaño de muestra para estimar una media y proporción poblacional cuando se conoce o no el tamaño de la población [imagen]. Tomada de Estadística II [Versión electrónica].



Donde:

N = tamaño de la muestra

N = tamaño de la población

S = desviación estándar

p = proporción muestral

q = 1-p e = error permitido

Z = nivel de confianza, expresado como valor del cuantil “z” de una distribución normal estándar, que separa la curva en dos áreas de tamaño 1 - α/2 y α/2 (0 < α < 1)

En la siguiente tabla se muestran los valores de “z” para distintos niveles de confianza:



Nivel de confianza z
90 % 1.64
95 % 1.96
99 % 2.58


El nivel de confianza asegura que el parámetro a estimar se encuentre en el intervalo de confianza, y se calcula su valor asociado para un valor “z” que se utiliza en las fórmulas anteriormente descritas.

Por ejemplo, para un nivel de confianza de 95 %, α = 1 - 0.95 = 0.05 y α/2 = 0.05/2 = 0.025. El cuantil z = 1.96 separa la curva normal estándar en dos regiones de tamaño 1 - 0.025 = 0.975 y 0.025.

Consulta la calculadora de valores “z”, sólo recuerda seleccionar la opción Two-Sided y al menos tres puntos decimales.

Ahora bien, con el propósito de mostrar los pasos a seguir para calcular una muestra a través del muestreo aleatorio simple, se presentan los siguientes ejemplos.

Población Lego


(s. a.) (2012). Lego [fotografía]. Tomada de https://pixabay.com/es/lego-mu%C3%B1eca-el-por-anfiteatro-de-1044891/



Caso 1. Estimar el ingreso medio

Calcular el tamaño de muestra que se requiere para estimar el ingreso medio de un despacho de consultoría de 90 empleados en nómina, donde se conoce que existe una desviación de $15 000. El tamaño de muestra debe garantizar un error de estimación máximo de $5000, con un nivel de significancia del 95 %.

Se identifican las siguientes variables:

N = 90 (población)

S = 15 000 (desviación estándar)

e = 5000 (error)

Z = 1.96 (nivel de significancia)

El ejercicio solicita calcular el ingreso medio, por lo tanto, habrá que utilizar la fórmula que obtiene una media para una población conocida (N), es decir:

desarrollo del caso 1


Rodríguez, A. y García, M. (2012). (2012). Desarrollo del caso 1 [imagen]. Tomada de Estadística II [Versión electrónica].



Caso 2. Grado de satisfacción

Se desea conocer cuál es el grado de satisfacción de los 3582 alumnos de primer ingreso de la Facultad de Contaduría y Administración de la UNAM, respecto al servicio de las ventanillas. En las últimas tres generaciones, esta aceptación fue del 40 %. Es necesario determinar a cuántos alumnos hay que entrevistar para garantizar un error máximo de 10 puntos porcentuales con un nivel de significancia del 90 %.

Se identifican las siguientes variables:

N = 3582 (alumnos)

P = 40 %, es decir: 0.40 (proporción muestral)

e = 10 %, es decir: 0.10 (error)

Z = 1.64 (nivel de significancia)

Dado que el parámetro que se busca estimar es una proporción, el tamaño de muestra se determina con la siguiente fórmula:

desarrollo del caso 2


Rodríguez, A. y García, M. (2012). Desarrollo del caso 2 [imagen]. Tomada de Estadística II [Versión electrónica].




Caso 3. Comercialización de aparatos electrónicos

Una empresa que comercializa aparatos electrónicos desea estimar el número promedio de aparatos que adquieren anualmente sus principales clientes. Se conoce que la desviación estándar es de 90 aparatos. Es necesario calcular el tamaño de muestra que garantice un nivel de confianza de 99 % con un error permitido de 10 piezas.

Se identifican las siguientes variables:

S = 90 (desviación estándar)

e = 10 (error en piezas)

Z = 2.58 (nivel de significancia)

Dado que no se conoce el tamaño poblacional y que el parámetro que se busca estimar es un promedio, el tamaño de muestra se determina con la siguiente fórmula:

desarrollo del caso 3


Rodríguez, A. y García, M. (2012). Desarrollo del caso 3 [imagen]. Tomada de Estadística II [Versión electrónica].



Caso 4. Proporción de vuelos

Históricamente, la proporción de vuelos demorados de una aerolínea es de 10 %. Los responsables de la aerolínea desean revisar los itinerarios de una muestra de vuelos del último año para comprobar si se sigue observando la misma proporción de demora.

Se pide calcular el tamaño de muestra que permita estimar la proporción de vuelos demorados en un año, con un nivel de confianza de 95 % y un error de tres puntos porcentuales.

Se identifican las siguientes variables:

P = 10 %, es decir: 0.10 (proporción muestral)

e = 3 %, es decir: 0.03 (error)

Z = 1.96 (nivel de significancia)

Como se desconoce el tamaño de la población y el parámetro que se busca estimar es una proporción, el tamaño de muestra se determina con la siguiente fórmula:

desarrollo del caso 4


Rodríguez, A. y García, M. (2012). Desarrollo del caso 4 [imagen]. Tomada de Estadística II. [versión electrónica].



Actividad. Muestreo aleatorio

La metodología del muestreo aleatorio simple nos permite estimar una proporción poblacional. Los datos obtenidos deben ser representativos para que los resultados sean certeros y con el menor margen de error posible.

En esta actividad debes identificar si las características que se exponen de la metodología del muestreo aleatorio simple son Falsas o Verdaderas; al contestar, considera los ejemplos revisados. Al finalizar podrás conocer tu desempeño.

Autoevaluación. Variables y fórmulas

Considerando los distintos elementos de la metodología del muestreo aleatorio simple, resulta esencial que se conozcan sus variables y fórmulas.

A continuación las deberás identificar, elige la opción correcta de acuerdo con la descripción proporcionada. Al finalizar podrás conocer tu desempeño.

Fuentes de información

Básicas

Bibliografía

Anderson, S. (2012). Estadística para negocios y economía (11.ª ed.). México: Cengage Learning.

Levin, R. y Rubin, D. (2010). Estadística para administración y economía (7.ª ed.). México: Pearson Educación.

Documentos electrónicos

Rodríguez, A. y García, M. (2012). (2012). Estadística II [Versión electrónica]. México: SUAYED-FCA-UNAM. Consultado el 10 de abril de 2018 de http://fcasua.contad.unam.mx/apuntes/interiores/docs/20172/contaduria/3/apunte/LC_1353_03106_A_estadisticaII.pdf

Complementarias

Lind, A. D., Marchal, G., W. y Wathen, S. (2012). Estadística aplicada a los negocios y economía (15.ª ed.). México: McGraw-Hill.


Cómo citar